Surface complexation
Surface Complexation is part of a free web series, GWB Online Academy, by Aqueous Solutions LLC.
What you need:
- GWB Professional recommended
-
Input files:
 3metals.x1t,
3metals.x1t,
 3Metals.x2t
3Metals.x2t
Download this unit to use in your courses:
- Lesson plan (.pdf)
- PowerPoint slides (.pptx)
Click on a file or right-click and select “Save link as…” to download.
Introduction
We begin our discussion of surface complexation with Irving Langmuir's work, which greatly improves upon the Kd and Freundlich isotherms. In the Langmuir model, a species sorbs and desorbs according to a reaction such as:
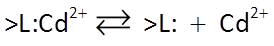
where >L:Cd2+ is a sorbing site occupied by a cadmium ion, and >L: is an unoccupied site.
The Langmuir reaction has an equilibrium constant K and a mass action equation:
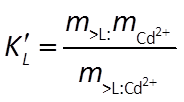
It additionally maintains a mass balance on the sorbing sites. The model, for this reason, does not predict that species can sorb indefinitely, since the number of sites available is limited
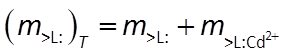
Combining the mass action and mass balance equations results in the Langmuir equation:
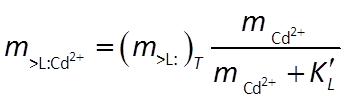
Where the concentration of Cd2+ is much smaller than K, the sorbed concentration varies in proportion to the concentration of the dissolved species. As the dissolved concentration increases to values greater than K, in contrast, the sorbed concentration approaches the concentration of sorbing sites, as shown below:
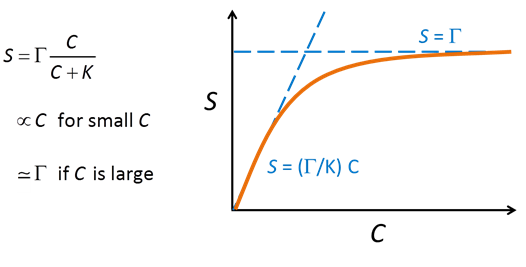
The Langmuir equation behaves very much like the Michaelis-Menten and Monod equations, described in the Biodegradation and Microbial Populations sections, respectively.
Experiments with natural sediments reveal a Freundlich-like nature to their isotherms, although the approach is purely empirical. A mechanistically based Langmuir model with multiple sorbing sites can reproduce this observation.
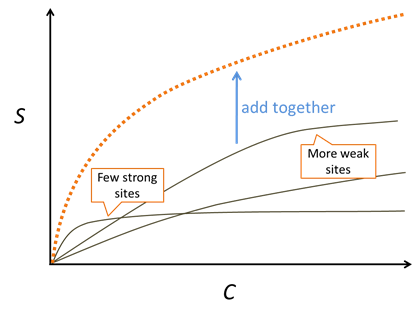
We consider a surface complexation model to be a multisite competitive Langmuir model that accounts for site protonation and deprotonation as well as electrostatic forces.
In order for an ion to sorb from solution, it must first move through an electrical potential field and then react chemically at the surface. Moving a positively charged ion toward a positively charged surface, for example, requires that work be done on the ion, increasing the system's free energy. An ion of the same charge escaping the surface would have the opposite energetic effect.
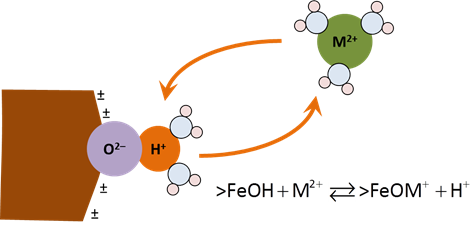
An equilibrium constant K represents the chemical effects of free energy. Multiplying K by the Boltzman factor (shown below) gives a complete account of the reaction's free energy.
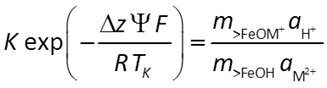
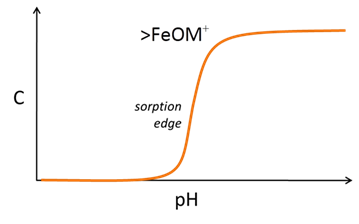
Three main classes of reactions are involved in surface complexation models. Each site can protonate or deprotonate to form surface species such as >FeOH2+ or >FeO−. In the absence of any complexing ions, the figure below explains the nature of surface sites and surface charge as a function of pH
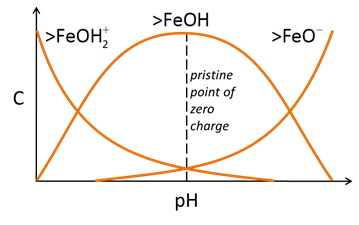
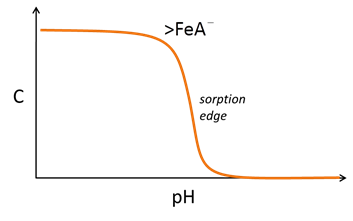
The sites can react with cations and anions from solution to form complexes, such as >FeOM+ or >FeA−. Increasing pH causes sites to deprotonate and complex with bivalent cations
Anion complexation, conversely, is typically favored at low pH
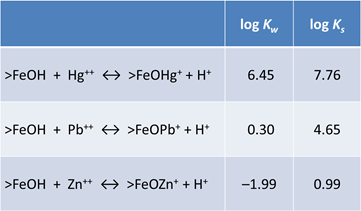
In this example, we'll use the compilation of surface complexation reactions from Dzombak and Morel (1990). They studied sorption onto hydrous ferric oxide (HFO = FeOOH · nH2O). Looking at the dataset, the sorbing sites are just like basis species in a thermo dataset. The two types of sites, strong and weak, give a Freundlich-like character to isotherms

Sorbing minerals can be associated with one or more sorbing sites. We use the mineral Fe(OH)3(ppd) as a proxy for HFO. According to the model, there are forty times more weak sites than strong sites

The strong sites can protonate, deprotonate, or complex cations. The weak sites can additionally complex anions

Task 1: Groundwater chromatography
Three heavy metal contaminants—Hg2+, Pb2+, Zn2+—pass into an aquifer in equal concentration. Sediment grains in the aquifer are coated with small amounts of hydrous ferric oxide, HFO or “rust”, onto which the contaminants can complex.
We'd like to construct a reactive transport model to show how the contaminants behave as they migrate with the flowing groundwater, accounting for the surface complexation.
To start, double-click on file “3metals.x1t”. The configuration is much like the simulation we've been tracing (“Pulse.x1t”), with the addition of two new contaminants and the HFO coatings.
Moving to the Initial pane
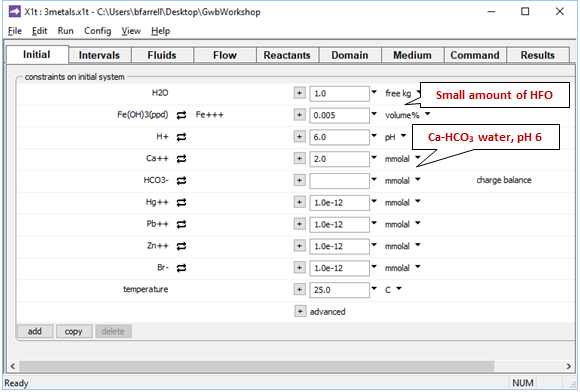
we see the aquifer contains a small amount of Fe(OH)3 precipitate, a proxy for HFO. The pore fluid is a Ca-HCO3 water, which provides a buffer in the simulation.
On the Fluids pane
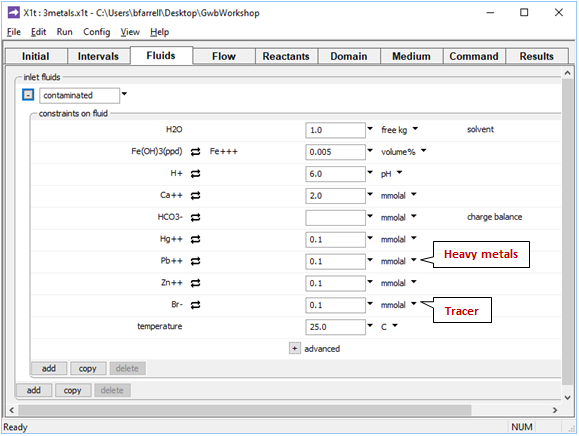
fluid passing into the domain contains 0.1 mmolal Hg2+ and Zn2+ contaminants, in addition to Pb2+. We've set the same concentration for Br−, which serves in the calculation as a tracer, since it neither reacts nor sorbs to HFO.
Opening Config → Sorbing Surfaces…, we see we've read in the “FeOH+.sdat” dataset
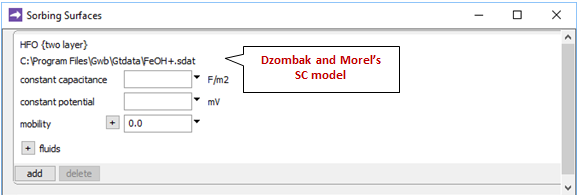
containing Dzombak and Morel's (1990) compilation of surface complexation reactions.
On the Config → Redox Couples… dialog
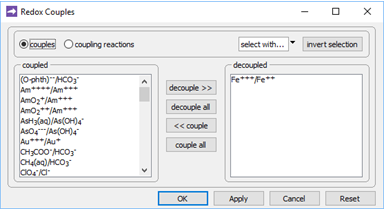
we see that redox coupling between ferric and ferrous iron has been disabled. This setting explains why we've been able to include Fe3+ species and minerals in the simulation, without setting basis entries representing Fe2+ or redox state.
Going to Config → Options…
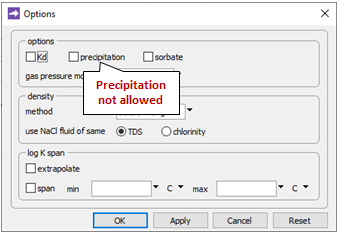
the “precipitation” option has been deselected. This setting prevents stable but slow-forming ferric minerals like goethite (FeOOH) from appearing in the simulation, at the expense of the Fe(OH)3 precipitate.
On the Config → Suppress… dialog
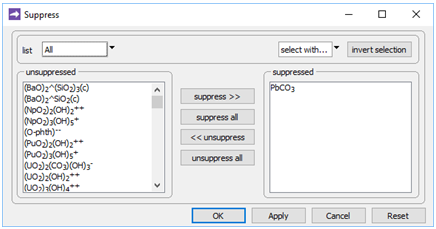
we've suppressed the PbCO3 ion pair, the stability of which in the database is almost certainly erroneous.
Finally, on Config → Output…, the suffix “_3metals” will be applied to datasets produced by the run

Trace the simulation by selecting Run → Go.
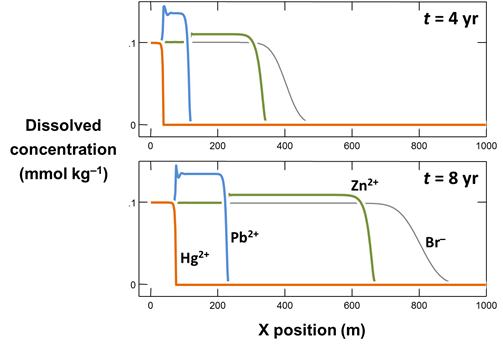
Use Xtplot to make a graph showing how the concentrations of the Hg2+, Pb2+, Zn2+, and Br− components vary along the aquifer, after 4 years and 8 years of reaction. Hint: double-click on the x-axis label and for “Display” choose “X position”
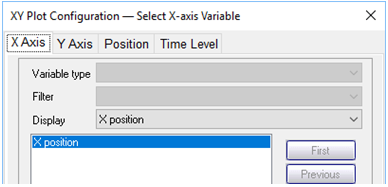
On the Y Axis pane choose “Components in fluid” and select Br−, Hg2+, and so on, with a linear axis. If it is not already selected, choose “Several values at one time” for “Display”
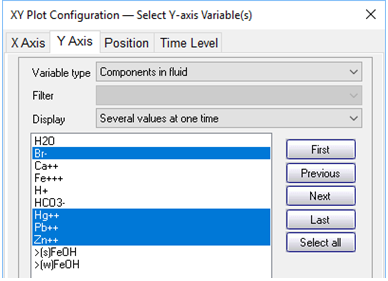
Why do Hg2+, Pb2+, Zn2+, and Br− migrate along the aquifer at different rates? Why at some points in the aquifer are Pb2+ and Zn2+ concentrations predicted to be greater than in the inlet fluid?
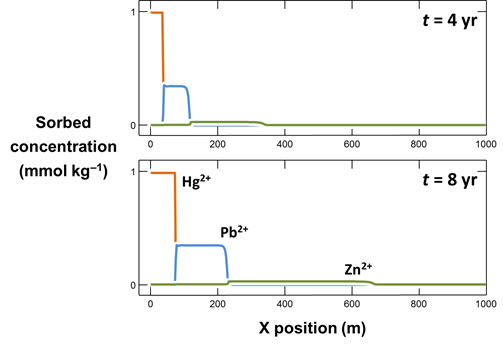
Make a second plot like the first, but showing the concentrations of sorbed Hg2+, Pb2+, and Zn2+ along the aquifer (Y Axis, “Components in sorbate”). Why do the contaminants segregate into zones as they sorb?
Task 2: Two dimensions
Let's try a more complex model. Three tanks leak Hg2+, Pb2+, and Zn2+ into an aquifer, where they are entrained by flow along the hydraulic grade.
After 10 years, the sources are controlled and a remediation well is installed down-gradient of the tanks to draw out contaminated groundwater. The remediation well is pumped in the simulation for 40 years.
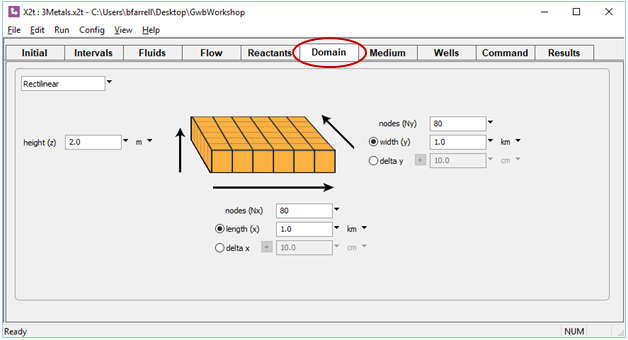
Start X2t by double-clicking on file “3metals.x2t”. On the Domain pane, we see the domain is 1 square km, divided into 6400 nodal blocks
On the Flow pane, we see the background discharge is 25 m yr−1, left to right
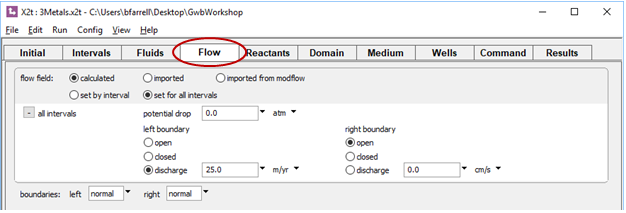
The Initial pane specifies a clean fluid
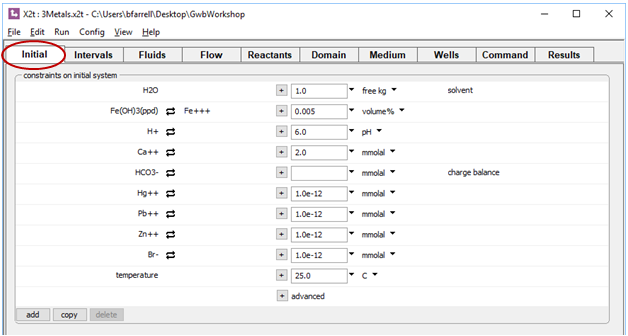
Four wells are defined on the Wells pane. Click  to expand any of the entries
to expand any of the entries
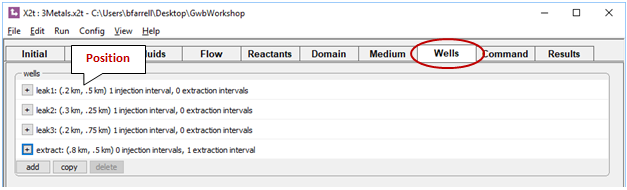
The first three slowly leak the “contamination” fluid into the aquifer over the first 10 years. The remaining well, at the bottom of the list, is the remediation well. It withdraws water from the aquifer, so the injection rate is set to a negative value
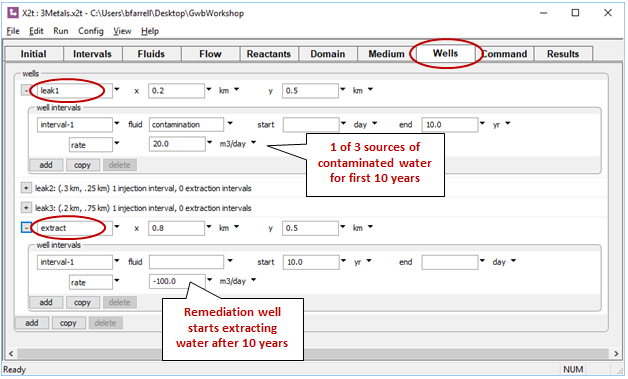
Fluid is withdrawn from the aquifer in the “extract” well, but none is injected, so no injectate chemistry need be specified.
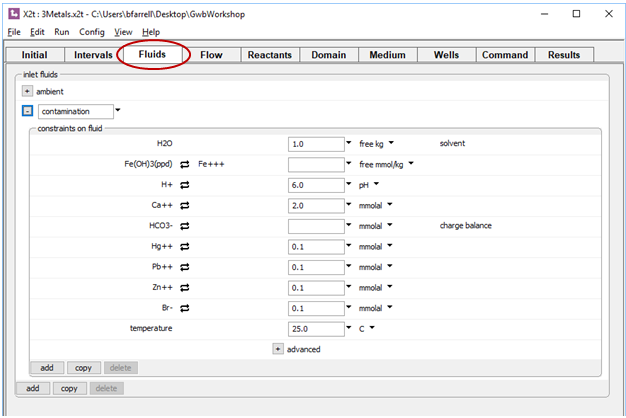
The Fluids pane is where we describe the chemistry of the fluids that will enter the domain over the course of the simulation. The first is a clean fluid, “ambient”, and the second is the comtaminated water that is laden with the inorganic metal pollutants as well as a bromide tracer
The Intervals pane specifies the duration of the simulation and the fluid crossing the left boundary
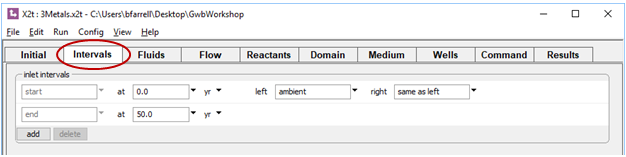
You can trace the simulation by selecting Run → Go.
We would like to make animations that show the equipotentials (contours of hydraulic potential) as well as the concentrations of tracer Br or one of the inorganic metal contaminants, Hg2+, Pb2+, or Zn2+.
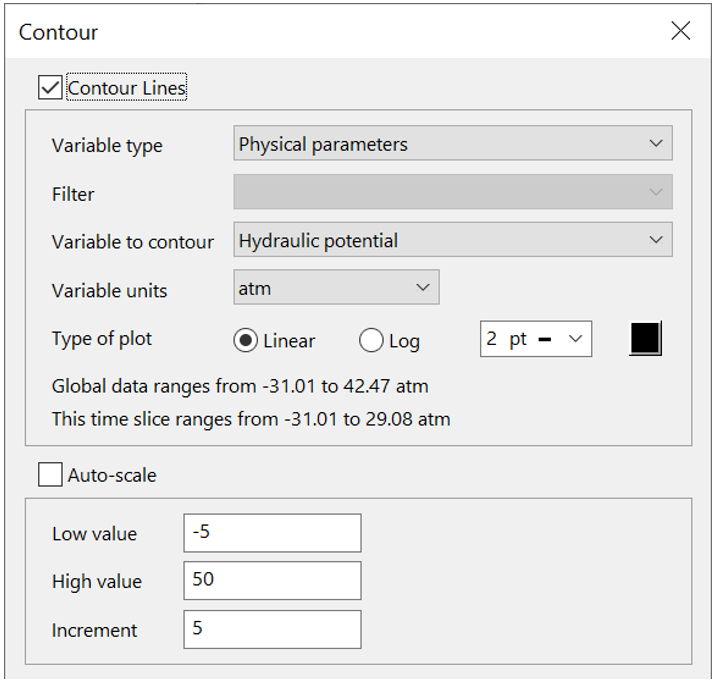
To do so, click  to launch Xtplot and go to Plot → Map View. To set up the equipotentials, go to Format → Contour..., choose “Physical parameters”, and select “Hydraulic potential”
to launch Xtplot and go to Plot → Map View. To set up the equipotentials, go to Format → Contour..., choose “Physical parameters”, and select “Hydraulic potential”
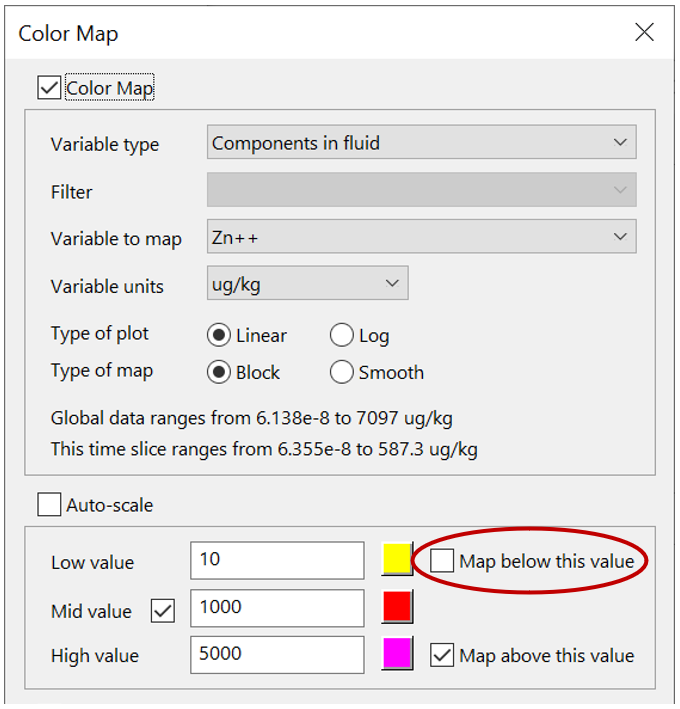
Color map the concentration of the tracer, or one of the metals, from Format → Color Map…, as you did in the previous exercise for sorbing solutes. Remember to select “Components in fluid” and the appropriate basis entry. Remember, you can mask areas of the domain that fall below the low value threshold by unchecking the “Map below this value” check box:
To add markers to your plot showing the well locations, go to Format → Wells…
Now, animate your diagrams from the Format → Animate… dialog
From your results, consider the following questions:
- How do the injection and production wells affect the flow field in each reaction interval?
- Why do Hg2+, Pb2+, Zn2+, and Br− migrate along the aquifer at different rates?
- How effective is flushing in removing each of the metals from the aquifer?
- Explain how surface complexation reactions can be both beneficial and a hindrance to remediation efforts.
Animation of two-dimensional example
In the simulation, three tanks leak water contaminated with heavy metals into an aquifer for 10 years. At that time, the leaks are controlled and an extraction well begins operation.
Three metals—Hg2+, Pb2+, and Zn2+—sorb in the run according to a surface complexation (two-layer) model, and Br− serves as a non-reactive tracer.
Authors
Craig M. Bethke and Brian Farrell. © Copyright 2016–2026 Aqueous Solutions LLC. This lesson may be reproduced and modified freely to support any licensed use of The Geochemist's Workbench® software, provided that any derived materials acknowledge original authorship.
References
Bethke, C.M., 2022, Geochemical and Biogeochemical Reaction Modeling, 3rd ed. Cambridge University Press, New York, 520 pp.
Bethke, C.M., B. Farrell, and M. Sharifi, 2026, The Geochemist's Workbench®, Release 18: GWB Reactive Transport Modeling Guide. Aqueous Solutions LLC, Champaign, IL, 191 pp.
Dzombak, D.A. and F.M.M. Morel, 1990, Surface Complexation Modeling. Wiley, New York, 393 pp.
Comfortable with Surface complexation?
Move on to the next topic, Mobile Colloids, or return to the GWB Online Academy home.