Sorbing solutes

Sorbing Solutes is part of a free web series, GWB Online Academy, by Aqueous Solutions LLC.

---

Introduction

The distribution coefficient approach—commonly referred to as the K_d approach—is the most widely applied method in environmental geochemistry for predicting the sorption of contaminant species onto sediments. The distribution coefficient K_d itself is simply the ratio under specific conditions of the sorbed to the dissolved mass of a contaminant. In other words,

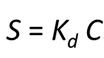
where S is the sorbed concentration, in moles per gram dry sediment, K_d is the distribution coefficient, in units of cm³ per gram, and C is the solute concentration, in moles per cm³.

The approach implies a reaction such as

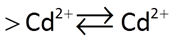
By the Freundlich method, another empirical approach,

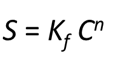
where K_f is the Freundlich coefficient, and n is the Freundlich exponent, which can range from 0 to 1. The Freundlich approach simply reduces to the linear K_d when the Freundlich exponent is 1.

The figure below shows sorption of selenate to a soil, showing mass sorbed per gram of dry soil, as a function of concentration in solution. Lines are fits to the data using the activity K_d, activity Freundlich, and Langmuir approaches

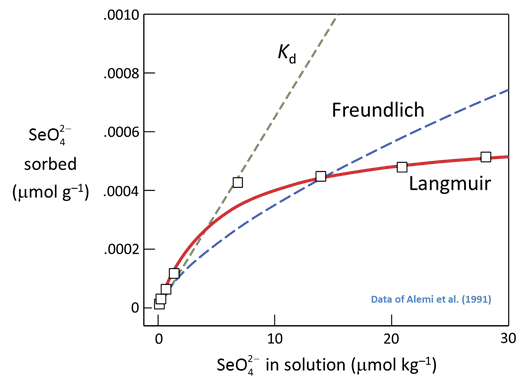
As can be seen, sorption by the K_d approach is equally effective at any concentration, whereas the exponent n in the Freundlich approach predicts progressively less effective sorption as concentration increases.

The activity K_d and activity Freundlich models (also known as reaction K_d and reaction Freundlich) that are coded into geochemical modeling software like The Geochemist's Workbench differ from the general approach:

where a is the activity of the free species and K_d' and K_f' account for the ion activity coefficient and ionized fraction of a component. Coefficients calculated in the traditional manner, therefore, need to be corrected by a factor of the species' activity coefficient. Care should be taken to apply them only to systems similar to that for which they were originally determined.

---

Task 1: K_d approach

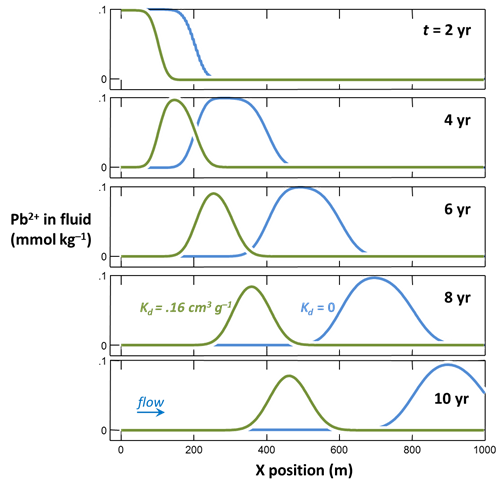
In a test, sediment from the aquifer sorbed Pb²⁺ according to a distribution coefficient K_d of .16 cm³ g^–1. The concentration of dissolved lead in the test was about 10 µmolar. Our job is to revise our model of Pb²⁺ transport in the aquifer to account for sorption.

The activity coefficient for Pb²⁺ in our groundwater is about .66, and the free ion makes up 80% of dissolved Pb, so the distribution coefficient K_d' for the activity K_d model works out to .30×10^–3 mol g^–1.

To set up the model, double-click once again on file “Pulse.x1t”. In X1t, go to File → Open → Sorbing Surfaces… (or Config → Sorbing Surfaces…), then navigate to the course directory and select file “Pb-Kd.sdat”, then close the Sorbing Surfaces dialog

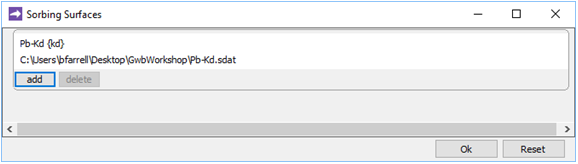
You can confirm you've pulled in the correct value for K_d' by clicking on File → View and selecting “.\Pb-Kd.sdat”.

Now, set “_Kd” as the suffix

and select Run → Go to trigger the calculation. Graph the results with Xtplot, as before.

How does sorption affect Pb²⁺ migration in the aquifer? The amount of Pb²⁺ dissolved in groundwater there?

show results hide results

We can calculate a retardation factor R_F

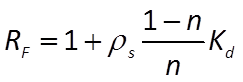
where n is porosity, and ρ_s is sediment density. Since porosity is 30% in our case, if we take a density of 2.65 g/cm³, the R_F is about 2. As you can see from the plot, the pulse migrates at about half the velocity of a non-reacting solute.

---

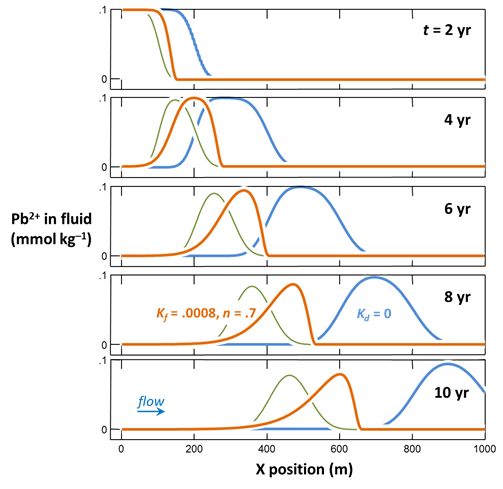
Task 2: Freundlich isotherm

Repeating the test using differing amounts of lead, we find K_d varies depending on the Pb²⁺ concentration. To account for this observation, we fit the test results to a Freundlich isotherm with a K_f' of 9.5×10^–6 and an n_f of 0.7. The Freundlich parameterization is equivalent to the K_d approach at a Pb²⁺ concentration of 10 µmolar.

To run the Freundlich case, return in X1t to the Config → Sorbing Surfaces… dialog. Click on the entry for the “Pb-Kd.sdat” dataset so that it's highlighted, then press the delete key on your keyboard to remove it. Click on , then read in file “Pb-Freundlich.sdat”

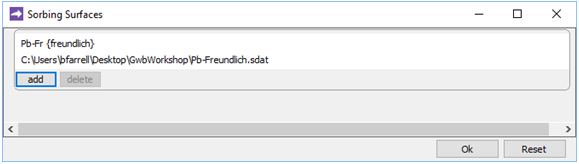
and close the dialog.

Set a suffix “_Freundlich”

and select Run → Go.

How did adopting a Freundlich isotherm affect the calculation results, compared to when we took the K_d approach to describe sorption?

show results hide results

---

Task 3: Two dimensions

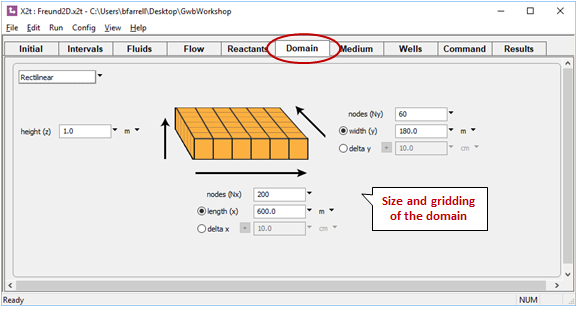
To carry the previous run into two dimensions, start program X2t by double-clicking on file “Freund2D.x2t”. Move to the Domain pane. Here, you can see the domain and how it's discretized

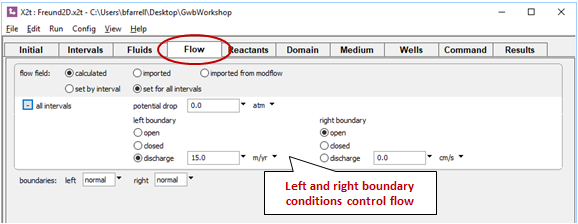
Move to the Flow pane. Here, you can see the boundary conditions for calculating the flow field, which moves from left to right

Move to the Wells pane

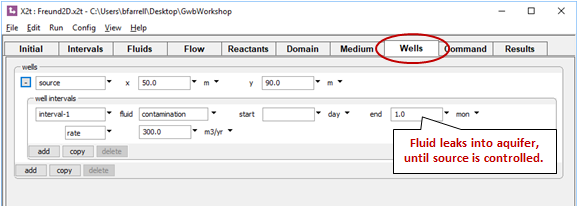
We've positioned a well toward the upstream end of the domain to introduce leakage from the contaminant source. Fluid from the well enters the aquifer during the first month of the simulation.

Examine the Initial pane. Here, we've set the aquifer to be filled with clean water initially

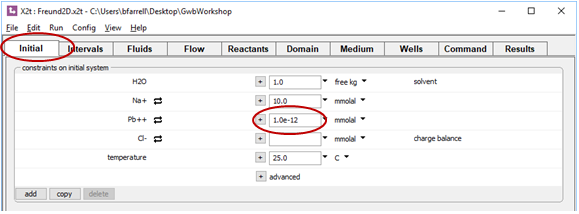
Check as well the Fluids pane. The “ambient” fluid is set to the same composition as the Initial fluid. The “contamination” fluid, in contrast, defines water contaminated with Pb²⁺

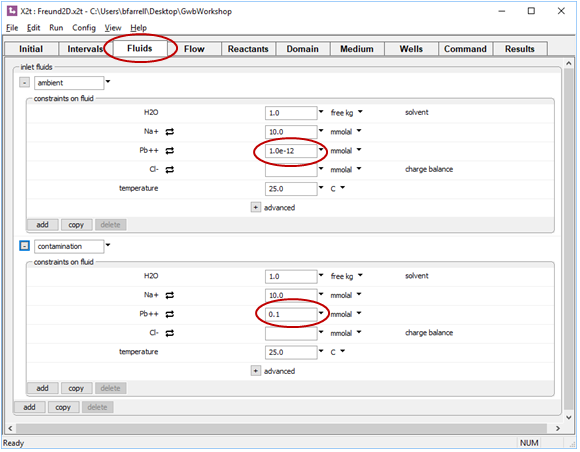
On the Intervals pane, we've associated the clean ambient water with the left side of the domain and set the duration of the simulation to 10 years

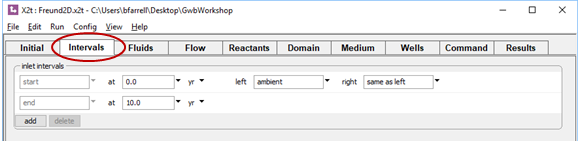
On the Medium pane, we've set the properties so that differential flow gives rise to dispersion. Porosity varies in a Gaussian distribution about 30%. The logarithm of permeability varies with porosity, so the permeability field is heterogeneous, too, and the resulting flow field is irregular

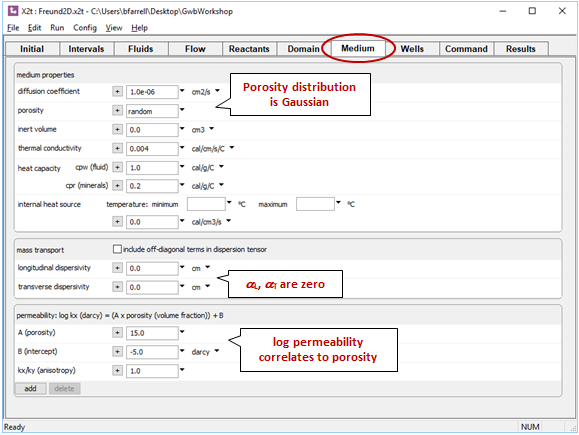
We're not using the Fickian concept of dispersion, so the values set for α_L and α_T from Fick's law are 0.

You can trace the simulation by selecting Run → Go.

To render the simulation results, click to launch Xtplot, and select Plot → Map View. Then chose Format → Color Map… , and in the top five fields choose: “Components in fluid”, “blank”, “Pb²⁺”, “ug/kg”, and “Linear”.

Uncheck “Auto-scale” and map low, mid, and high values to “15 µg/kg”, “100 µg/kg”, and “200 µg/kg”. Now, associate the values with yellow, red, and magenta.

To mask areas of the aquifer where Pb²⁺ concentration falls below the USEPA's MCL of 15 µg/kg, uncheck “Map below this value”. The program will mask values in the range 0 to 15 µg/kg using the color white. When you're done, the dialog should look like this:

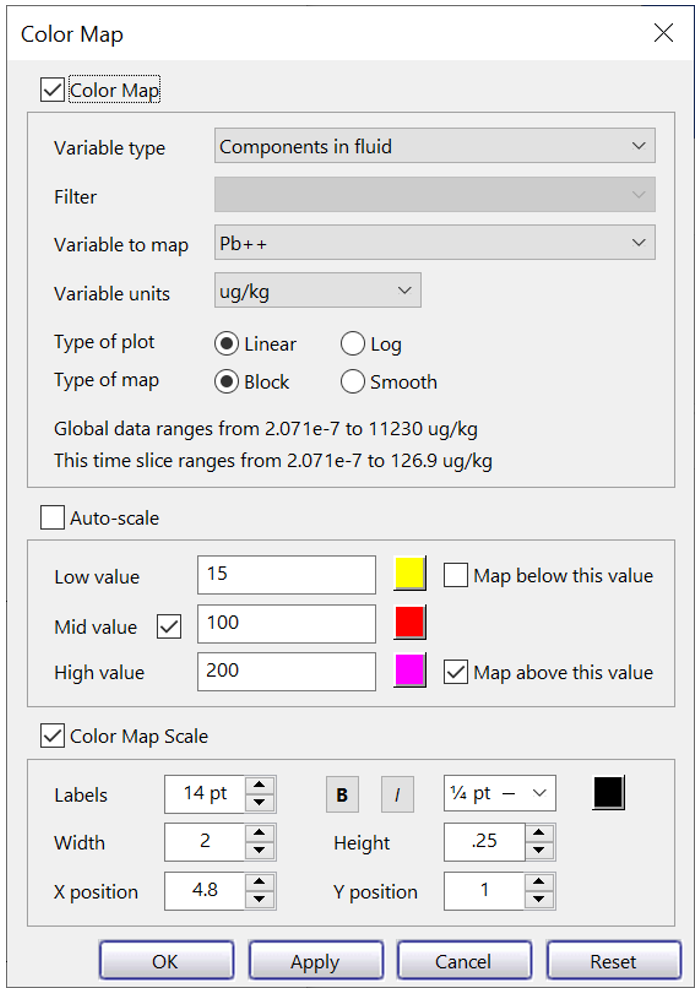
Click OK.

Now, click on Format → Time Step…

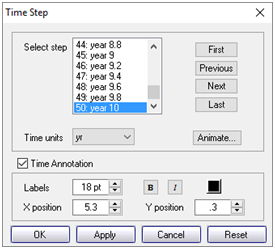
choose a time to render and click Apply. You can move forward and backward in time with the Next and Previous buttons.

Finally, click on and on the dialog that pops up

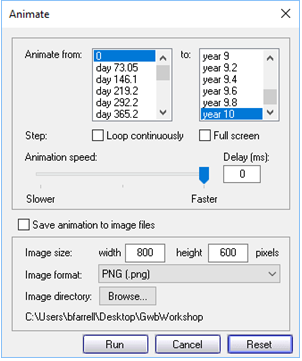
click Run.

Note the “Loop continuously” and “Full screen” check boxes. Note further the “Save animation to image files” check box. We will use this option to save the frames from which we'll make video clips of our animations.

---

Animation of two-dimensional example

Animations in this movie show a simulation of Pb²⁺ transport through a heterogeneous medium, accounting for contaminant attenuation by sorption to the aquifer solids. There is a series of three simulations:

• The non-reacting case, for reference
• The lead ion sorbs according to a distribution coefficient K_d
• Sorption follows a Freundlich isotherm

---

Authors

Craig M. Bethke and Brian Farrell. © Copyright 2016–2024 Aqueous Solutions LLC. This lesson may be reproduced and modified freely to support any licensed use of The Geochemist's Workbench® software, provided that any derived materials acknowledge original authorship.

References

Alemi, M.H., D.A. Goldhamer and D.R. Nelson, 1991, Modeling selenium transport in steady-state, unsaturated soil columns. Journal of Environmental Quality 20, 89–95.

Bethke, C.M., 2022, Geochemical and Biogeochemical Reaction Modeling, 3^rd ed. Cambridge University Press, New York, 520 pp.

Bethke, C.M., B. Farrell, and M. Sharifi, 2024, The Geochemist's Workbench®, Release 17: GWB Reactive Transport Modeling Guide. Aqueous Solutions LLC, Champaign, IL, 191 pp.

---