Dual porosity

Dual Porosity is part of a free web series, GWB Online Academy, by Aqueous Solutions LLC.

---

Introduction

Bypassing is a common problem in environmental hydrology, as it often undermines active remediation strategies. As water flows through an aquifer, it commonly bypasses low conductivity sediments, or stagnant zones. Solute can, however, diffuse into or out of these stagnant zones, depending on the relative concentrations of solute in the high and low conductivity zones of the aquifer.

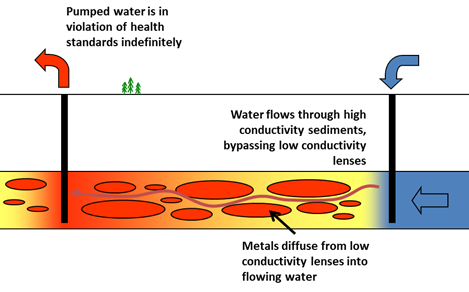
In remediating an aquifer by the pump and treat method, all the produced water comes from the high-conductivity, or free-flowing zones. Clean water flushed through the aquifer can become contaminated as solute diffuses out of the stagnant zones into the water.

A dual porosity model can account for the effects of preferential flow, bypassing, and solute exchange. In the model, each nodal block is divided into free-flowing and stagnant fractions. Water is transported from one node to the next only within the free-flowing fraction. Within a nodal block, however, solute diffuses from the free-flowing fraction into and out of stagnant zones.

The geometry of a stagnant zone can be described by spheres, blocks, or fractures, but the controlling factor is contact area. You set a stagnant fraction X_stag, and radius r or half-width δ of stagnant spheres or blocks. You can also set D*, N_subnode, δ_diff, R_F, and so on.

Each nodal block in a dual porosity model, assuming the spherical geometry, looks like this

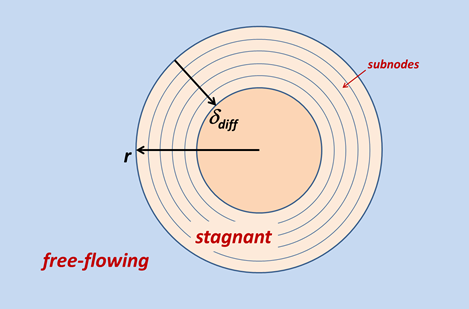
where r is the radius of the stagnant zone. The stagnant fraction and radius set the surface area over which diffusion occurs. The stagnant zone is divided into a number of subnodes extending from the free-flowing zone–stagnant zone interface to the center of the sphere. The diffusion equation is solved along this coordinate, or if the diffusion length δ_diff is set, within only the outer skin of the stagnant zone.

---

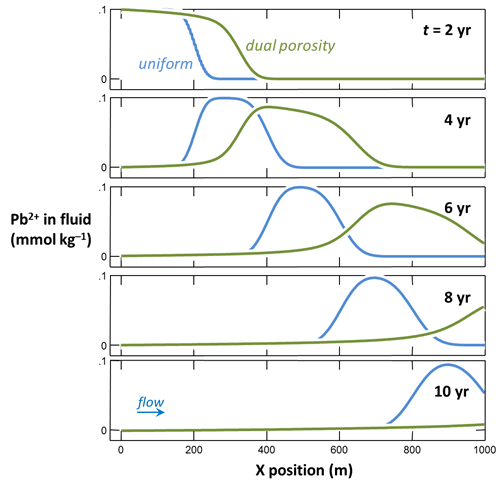
Task 1: Dual porosity model of Pb transport

We'll model Pb transport as before, except we'll take 40% of the aquifer to be stagnant. Water is stationary there, but the contaminant can diffuse in from the free-flowing zone, and back out. The stagnant zones in the model have a characteristic radius of 1 meter. In light of the diffusion length 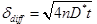corresponding to a time span of 10 years, we'll trace diffusion within only the zones' outer 20 cm.

Open file "Pulse.x1t". Start the Config → Dual Porosity… dialog and configure the dual porosity feature as shown

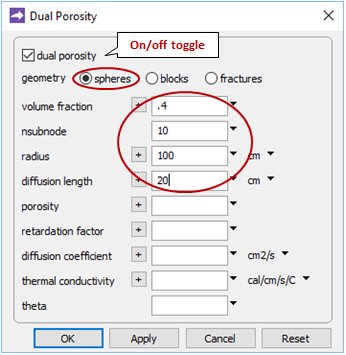
Click OK. Set a suffix "_dual" (Config → Output…)

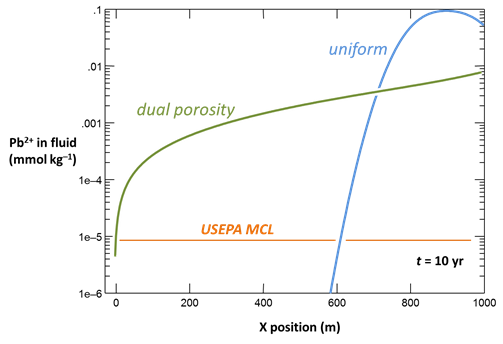
and click OK. Click on Run → Go to execute the simulation, then render the results with Xtplot. How do they differ from a single porosity simulation?

show results hide results

Here's a video of the X1t setup

---

Animation of two-dimensional example

This movie shows the results of X2t simulations of the migration of inorganic Pb through an aquifer. A dual porosity model accounts for diffusion into and out of stagnant zones in the aquifer. There are three simulations:

• A single porosity model for a uniform medium, for reference
• A dual porosity simulation in which stagnant zones with a characteristic dimension of 1 m occupy 40% of the aquifer
• The dual porosity model above, applied to a heterogeneous aquifer

---

Authors

Craig M. Bethke and Brian Farrell. © Copyright 2016–2024 Aqueous Solutions LLC. This lesson may be reproduced and modified freely to support any licensed use of The Geochemist's Workbench® software, provided that any derived materials acknowledge original authorship.

References

Bethke, C.M., B. Farrell,and M. Sharifi, 2024, The Geochemist's Workbench®, Release 17: GWB Reactive Transport Modeling Guide. Aqueous Solutions LLC, Champaign, IL, 191 pp.

---