Redox disequilibrium
Redox Disequilibrium is part of a free web series, GWB Online Academy, by Aqueous Solutions LLC.
What you need:
- GWB Essentials recommended
-
Input file:
 microbe.sp8
microbe.sp8
Download this unit to use in your courses:
- Lesson plan (.pdf)
- PowerPoint slides (.pptx)
Click on a file or right-click and select “Save link as…” to download.
Introduction
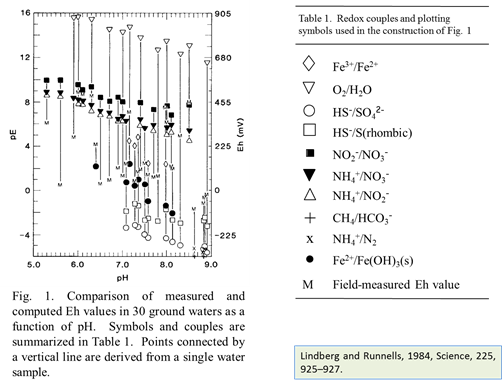
At low temperature many redox reactions are unlikely to achieve equilibrium. Lindberg and Runnells (1984) demonstrated the generality of this problem. They compiled more than 600 water analyses that provided at least two measures of oxidation state and calculated species distributions for each sample. They then computed redox potentials for the various redox couples in the analysis, using the Nernst equation. Their results showed that redox couples in a sample generally failed to achieve equilibrium with each other.
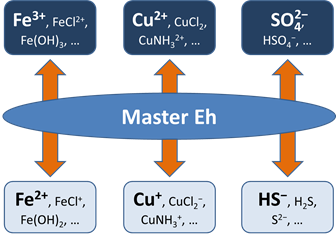
Before this idea was widely accepted, the common approach in geochemical modeling was to assume that all redox reactions reached equilibrium. The user sets a single value for the system oxidation state, or a “Master Eh,” which controls the distribution of species among different oxidation states.
A more realistic approach is to allow for redox disequilibrium by disabling one or more redox coupling reactions. All coupled redox reactions still reflect the Master Eh for the system. Disabled redox couples, though, behave independently.
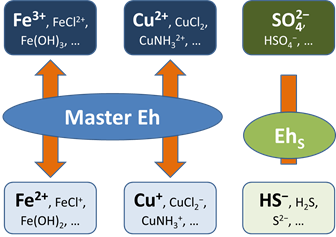
Any number of redox coupling reactions can be disabled.
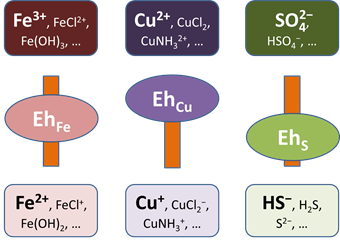
For any disabled couple, you can write out an electron transfer reaction and calculate the Nernstian Eh. Where redox equilibrium is not achieved, each disabled couple would have a distinct Nernstian Eh.
In this lab we will consider how to construct chemical models that account for redox reactions that are not in thermodynamic equilibrium. The GWB programs allow you to interactively control which redox couples are to be held in equilibrium and which are not.
Disabling the redox couple between Fe+++ and Fe++, for example, eliminates any provision for equilibrium between ferrous and ferric iron. Species Fe+++ is available as a new entry in the basis, which you can constrain independently from Fe++. Going to the Basis pane, you will find that you can now add Fe+++ to the basis list.
This feature is quite useful—and commonly necessary—for modeling natural waters. You will likely find yourself decoupling sulfide from sulfate, methane from carbonate, ammonium and nitrite from nitrate, As(V) from As(III), and so on.
Task 1: Chemical energy in natural waters
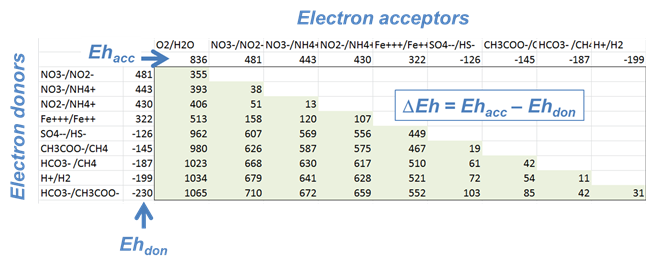
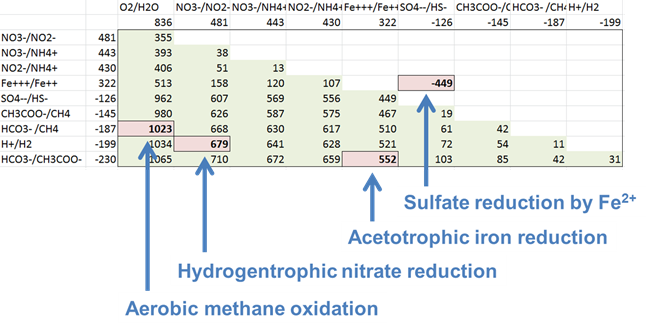
Microbes take advantage of the redox disequilibrium found in the natural environment to derive energy. Respiring microbes trap energy released when electrons liberated by an electron-donating reaction are taken up by an electron-accepting reaction.
The difference ΔEh between the Eh for the accepting and donating reactions is a measure in volts or mV of the energy released. The value is given as
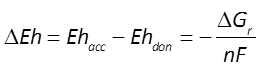
where n is the number of electrons transferred and F is the Faraday constant. Reactions with positive ΔEh values release energy.
Double-click on file “microbe.sp8”. When SpecE8 opens, move to the Basis pane
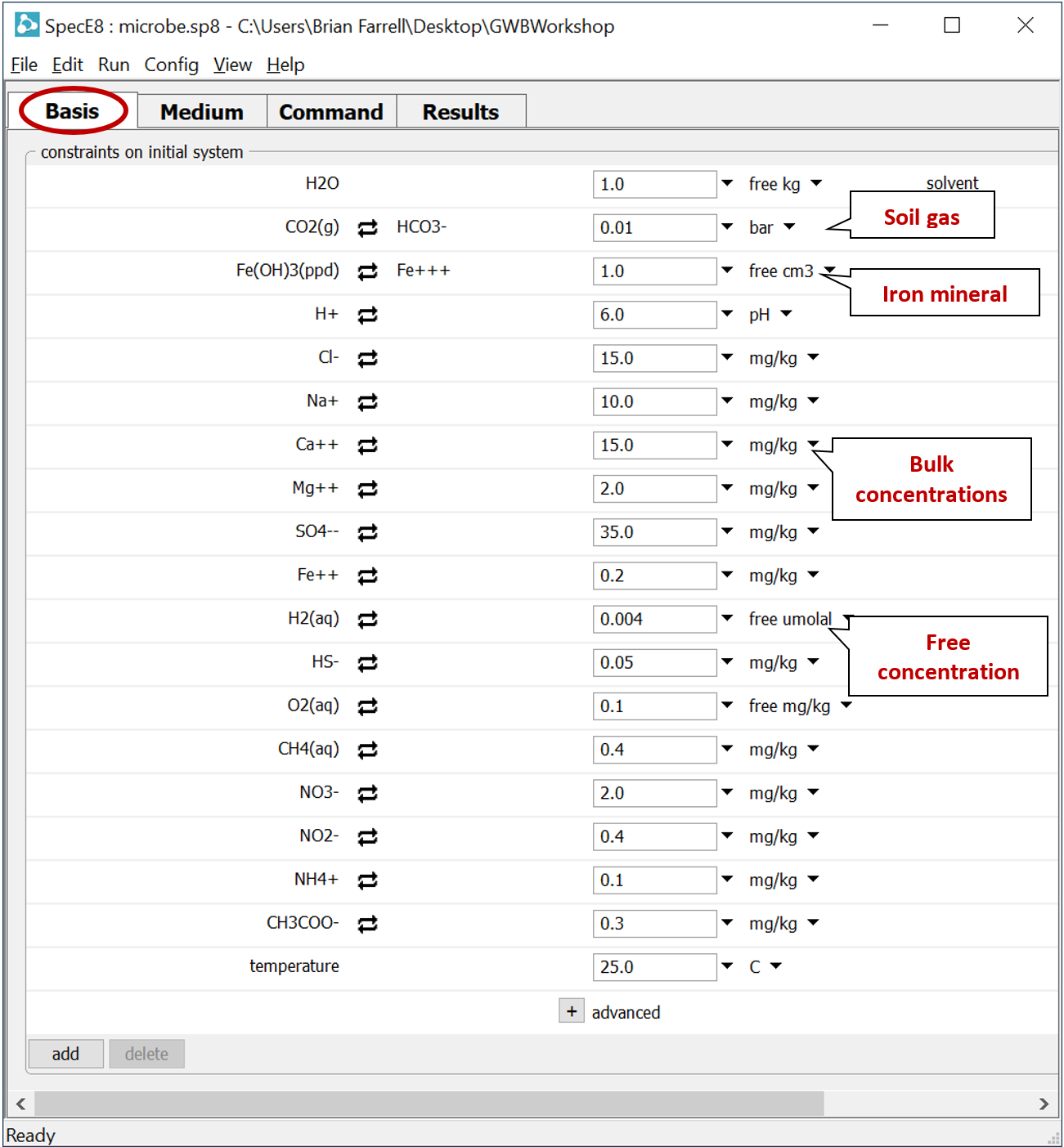
The input describes the analysis of a hypothetical groundwater, assuming equilibrium with ferric hydroxide and a soil gas in which PCO2 = 10−2. Note that constraints are provided for the distribution of several elements across differing redox states.
To see why, open the Config → Redox Couples… dialog
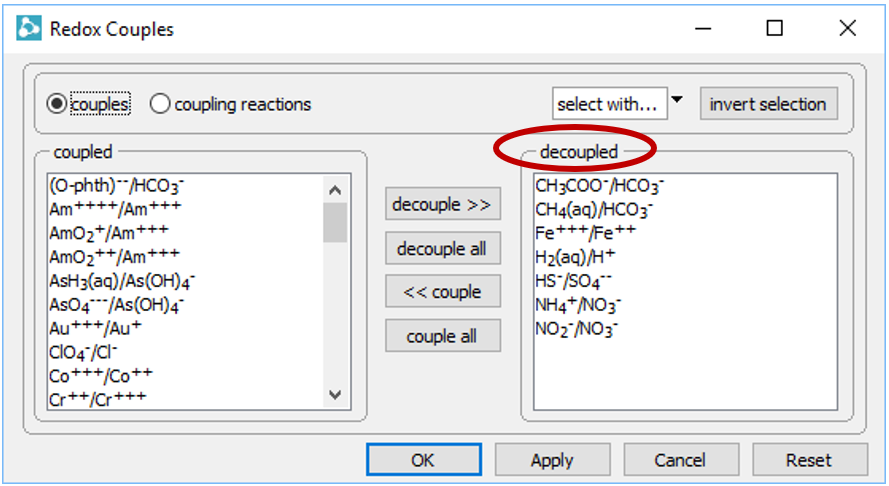
Several redox pairs have been disabled.
Move to the Results pane and click  , then click
, then click 
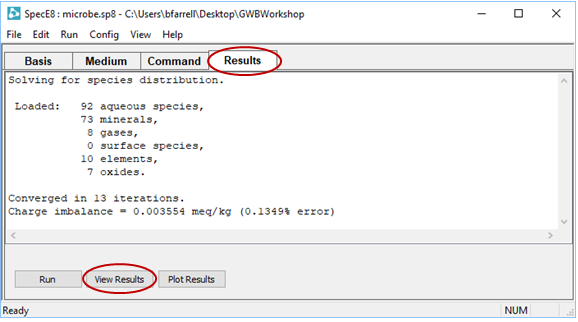
In SpecE8's output file, check the Nernst Eh values for the following redox couples:
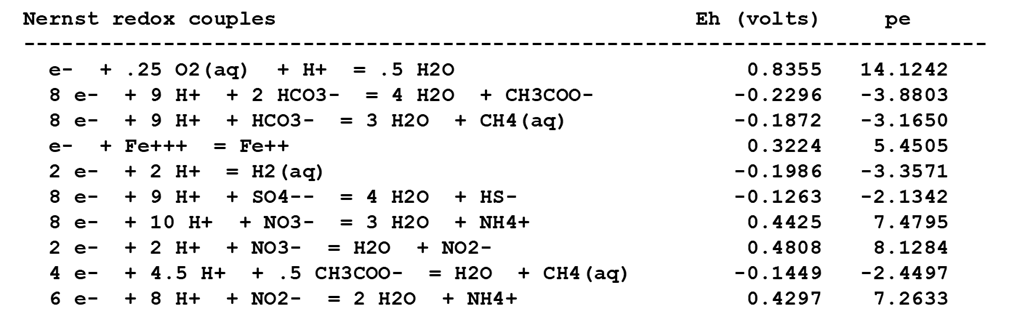
Which couple is the most energetically favorable as an electron-donating reaction? Which is the best at accepting electrons?
For each of the following metabolisms, determine ΔEh. Which metabolisms are favorable for microbes living in contact with this groundwater?
- Oxidation of acetate by ferric iron
- Oxidation of methane by molecular O2
- Reduction of sulfate by ferrous iron
- Oxidation of H2 by nitrate
Authors
Craig M. Bethke and Brian Farrell. © Copyright 2016–2026 Aqueous Solutions LLC. This lesson may be reproduced and modified freely to support any licensed use of The Geochemist's Workbench® software, provided that any derived materials acknowledge original authorship.
References
Bethke, C.M., 2022, Geochemical and Biogeochemical Reaction Modeling, 3rd ed. Cambridge University Press, New York, 520 pp.
Bethke, C.M., B. Farrell, and M. Sharifi, 2026, The Geochemist's Workbench®, Release 18: GWB Essentials Guide. Aqueous Solutions LLC, Champaign, IL, 232 pp.
Lindberg, R.D. and D.D. Runnels, 1984, Groundwater redox reactions: an analysis of equilibrium state applied to Eh measurements and geochemical modeling. Science 225, 925–927.
Comfortable with redox disequilibrium?
Move on to the next topic, High-salinity Fluids, or return to the GWB Online Academy home.