Equilibrium models

Equilibrium models is part of a free web series, GWB Online Academy, by Aqueous Solutions LLC.

---

Introduction

We consider here how dissolved species are distributed in natural waters, and the relationship of the species distribution to mineral saturation and gas fugacity.

We'll also consider how to construct chemical models that account for redox reactions that are not in thermodynamic equilibrium. The GWB programs allow you to interactively control which redox couples are to be held in equilibrium and which are not.

---

Task 1: Species distribution in natural waters

To calculate a chemical model of a groundwater sample, we'll define the measured bulk composition of the fluid and enter values for the partial pressures of soil gases and the mass of minerals in contact with the fluid. Double-click on file “microbe.sp8”. When SpecE8 opens, move to the Basis pane

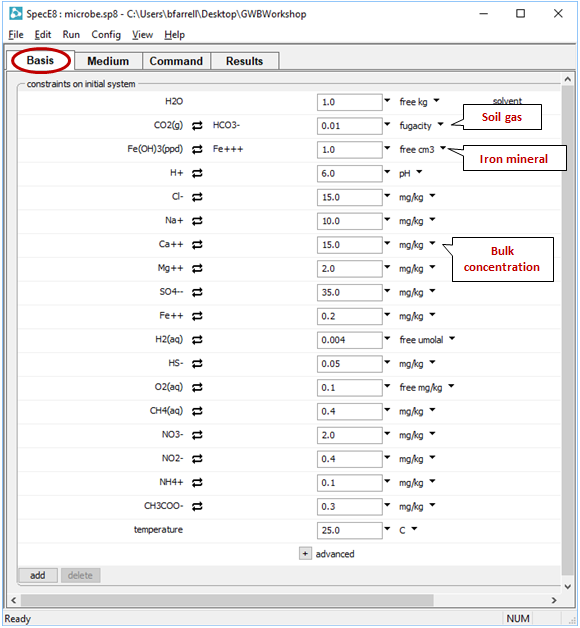
The input describes the analysis of a hypothetical groundwater, assuming equilibrium with ferric hydroxide and a soil gas in which f CO₂ = 10⁻². Note that constraints are provided for the distribution of several elements across differing redox states.

To see why, open the Config → Redox Couples… dialog

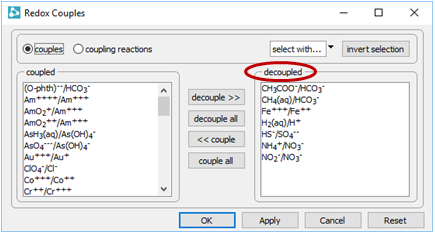
Several redox pairs have been disabled.

Move to the Results pane and click , then click

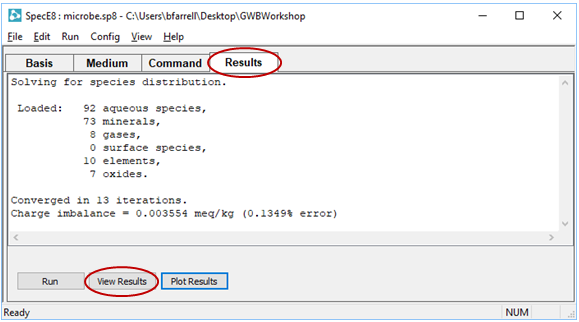
Take a moment to look through the dataset, and locate the following information:

• The system's pH and oxidation state
• The mass of solvent and solution (why are they different?)
• The species' concentrations, activities, and activity coefficients
• The saturation states of various minerals
• The fugacities of various gases
• The system's bulk composition

The activities of aqueous species can be thought of as thermodynamic concentrations. By how much do the activities calculated for species in the groundwater differ from molal concentrations?

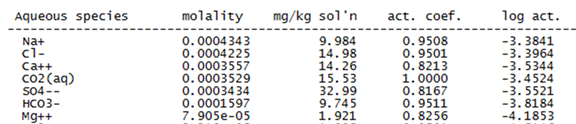
The principle of mass balance requires that the concentrations of the species containing any component (i.e., Cl−) add up to the component's analytical concentration. We call the molalities of individual species “free concentrations,” and refer to the analytical concentrations of the components in solution as “total concentrations.”

You can verify that SpecE8 honors the principle of mass balance by adding the molalities of the species containing a given component (but not species concentrations in mg kg⁻¹, since the mole weight of each species differs).

The fastest way to add the species' concentrations is to export the numerical values from the plotted results into MS Excel. In SpecE8, click to launch Gtplot and configure a diagram as indicated below

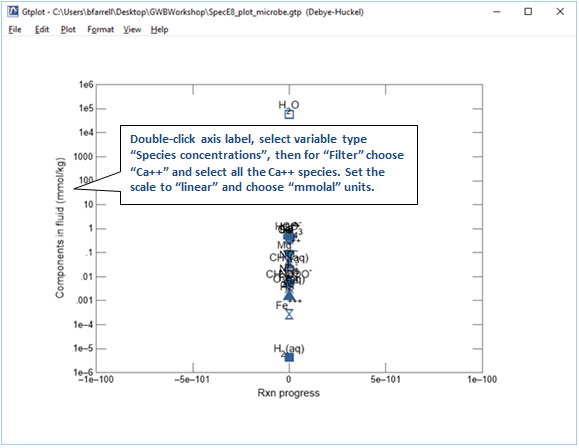
Your diagram should look like this. To get the numerical values, select Edit → Copy

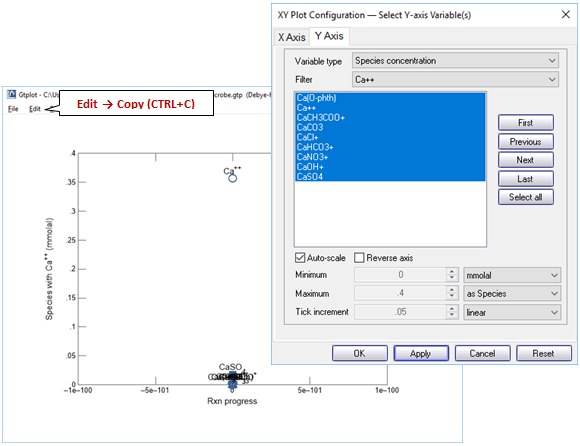
then paste into MS Excel

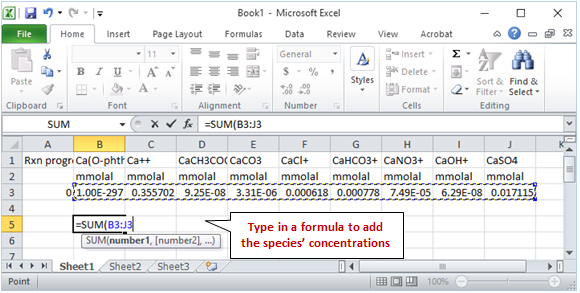
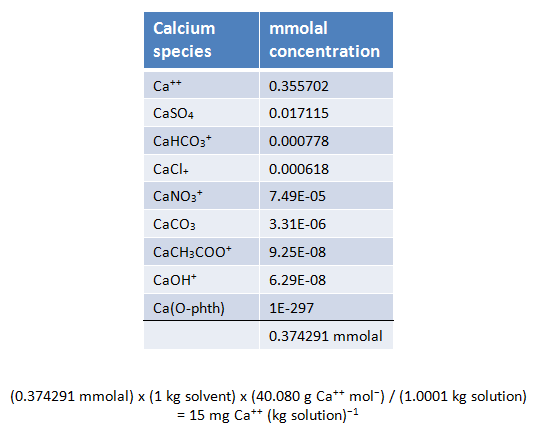
The SUM function will quickly calculate the total concentration of calcium species.

The example below demonstrates mass balance for the calcium component

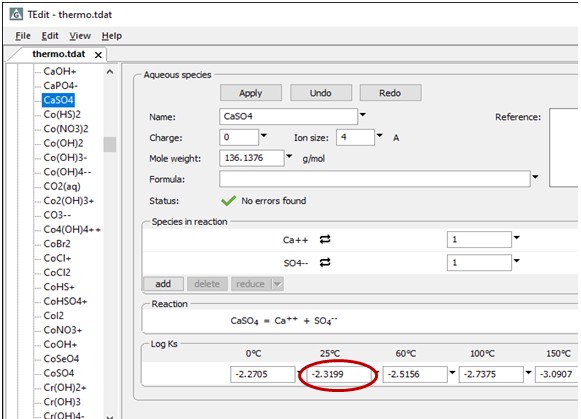
The principle of mass action requires that any possible reaction among the species be at its equilibrium point. You can extract reactions and associated equilibrium constants from the thermo dataset. Select File → View → .\thermo.tdat to inspect the dataset in TEdit, the graphical thermo data editor.

To demonstrate that a reaction is in equilibrium, you show that the reaction's activity product matches its equilibrium constant. Below is the reaction and equilibrium constant at 25°C for the calcium-sulfate ion pair as it appears in “thermo.tdat”:

Returning to the results file, we can find the activity of the Ca⁺⁺, SO₄⁻⁻, and CaSO₄ species in our modeled fluid

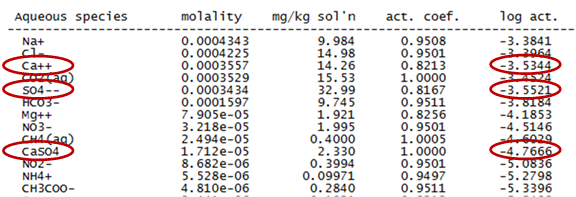
With this information, we can write out the mass action equation and substitute in the species' activities to calculate the activity product, Q

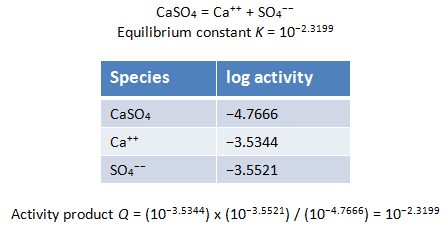
Comparing the activity product to the equilibrium constant, we find that the reaction is in equilibrium and mass action has been honored.

We generally think of mineral saturation in terms of a fluid's saturation index (or S.I.) with respect to a particular mineral. The saturation index is the logarithm of the ratio of the activity product to the equilibrium constant for the reaction to form the mineral in question: S.I. = log Q/K

When a mineral has equilibrated with a fluid, Q equals K and the saturation index is 0. S.I. values less than 0 indicate undersaturation, and those greater than 0 show supersaturation. We constrained the ferric iron component in our model by swapping the mineral Fe(OH)₃(ppd) into the basis. Does the S.I. of the mineral indicate our constraint has been honored?

Because we've decoupled several redox pairs, we've prescribed a state of redox disequilibrium in our model. We can verify that the various sulfate species are in equilibrium with each other (as we did for the calcium-sulfate ion pair and the sulfate ion), as are the sulfide species, but sulfate is not in equilibrium with sulfide. Similarly, ferric iron species are in equilibrium with themselves, as are ferrous iron species, but ferric iron and ferrous iron are not in equilibrium with each other.

Below is an example of a reaction between a decoupled redox pair. Does the reaction appear to be in equilibrium?

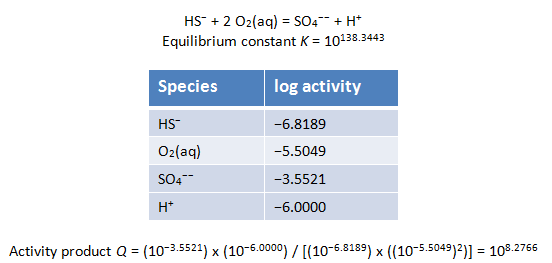
SpecE8 reports a value for Eh near the very top block of the output file, as well as several Nernst Eh values for decoupled redox pairs below. Given that we've prescribed a redox disequilibrium model, does it make sense that the various Eh values are all different?

---

Authors

Craig M. Bethke and Brian Farrell. © Copyright 2016–2024 Aqueous Solutions LLC. This lesson may be reproduced and modified freely to support any licensed use of The Geochemist's Workbench® software, provided that any derived materials acknowledge original authorship.

References

Bethke, C.M., 2022, Geochemical and Biogeochemical Reaction Modeling, 3^rd ed. Cambridge University Press, New York, 520 pp.

Bethke, C.M., B. Farrell, and M. Sharifi, 2024, The Geochemist's Workbench®, Release 17: GWB Essentials Guide. Aqueous Solutions LLC, Champaign, IL, 232 pp.

---