Dissolution and precipitation
Dissolution and Precipitation is part of a free web series, GWB Online Academy, by Aqueous Solutions LLC.
What you need:
- GWB Professional recommended
-
Input file:
 Quartz.x1t
Quartz.x1t
Download this unit to use in your courses:
- Lesson plan (.pdf)
- PowerPoint slides (.pptx)
Click on a file or right-click and select “Save link as…” to download.
Introduction
The GWB programs have a Built-in Rate Law for mineral dissolution and precipitation
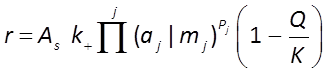
where r is the mineral's dissolution rate, AS is the surface area of the mineral, k+ is the intrinsic rate constant, aj, mj are the activity or concentration of promoting or inhibiting species, Pj is a species' power (+ is promoting, − is inhibiting), and Q and K are the activity product and equilibrium constant, respectively, for the dissolution reaction.
The user supplies parameters for the rate law, including a specific surface area and rate constant for each mineral. The rate constant can be set directly or it can be calculated from the activation energy EA and pre-exponential factor A using the Arrhenius equation
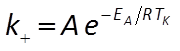
where R is the gas constant, and TK is absolute temperature.
Task 1: Quartz weathering
How rapidly does mineral dissolution affect the chemistry of water flowing along an aquifer composed of only quartz? Double-click on “Quartz.x1t” to calculate a reactive transport model of rainwater infiltrating such an aquifer.
The Initial pane
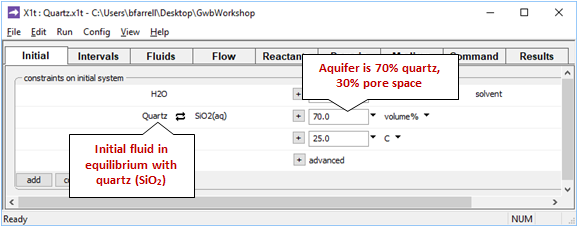
shows the conditions at the onset of the simulation.
On the Intervals pane
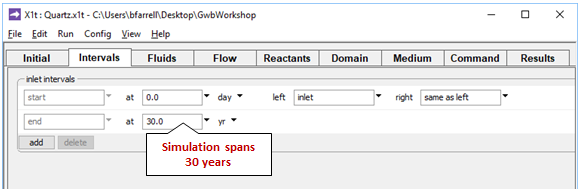
we set the model's time span and associate an inlet fluid with the domain's left side.
On the Fluids pane
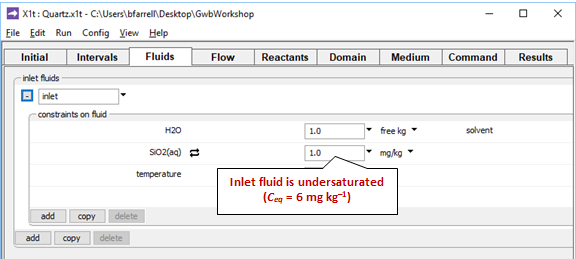
we define a fluid called “inlet”, the rainwater recharging the aquifer, which is set to be undersaturated with respect to quartz.
On the Reactants pane a kinetic law governs quartz dissolution
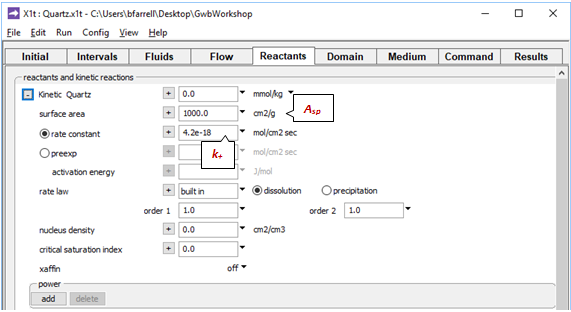
The rate constant k+ is from Rimstidt and Barnes (1980), and the specific surface area Asp is from Leamnson et al. (1969). The mass of quartz carried in the simulation is the amount of buffering mineral shown in the Initial pane, plus the mass set in the Reactants pane, which here is 0.
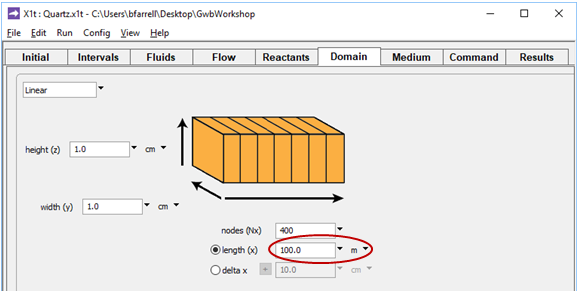
On the Domain pane, aquifer length is set to “100 m”
and on the Flow pane
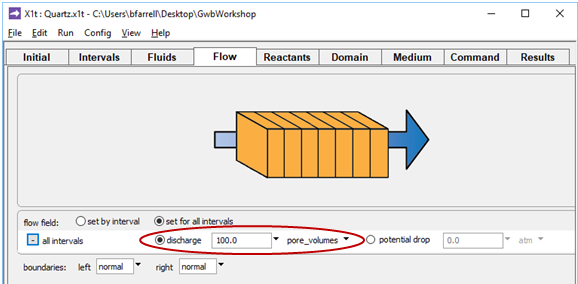
the simulation is configured to displace the pore fluid in the aquifer 100 times. Because the simulation spans 30 years, groundwater velocity vx is (100 m)/(30 yr/100), or 330 m yr−1.
Note the suffix

and select Run → Go to calculate the model.
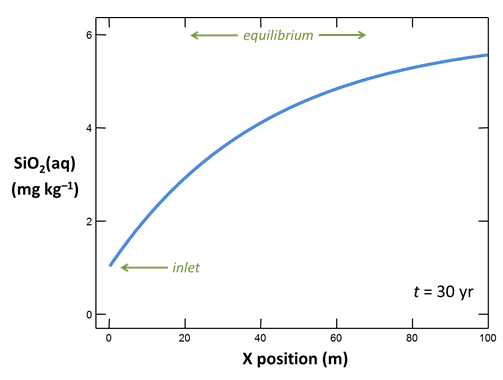
On the Results pane, click on  and graph the concentration in mg kg−1 of SiO2(aq) in the fluid against position in the aquifer. Choose the time step at the end of the simulation, t = 30 years.
and graph the concentration in mg kg−1 of SiO2(aq) in the fluid against position in the aquifer. Choose the time step at the end of the simulation, t = 30 years.
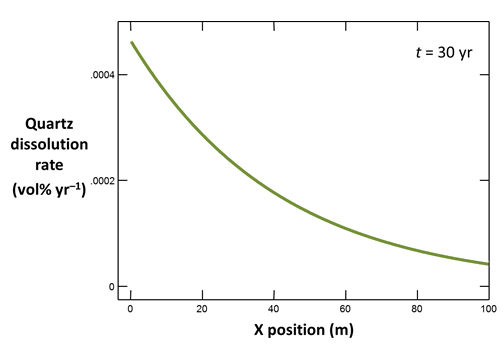
Return to X1t and click on  once again to open a second instance of Xtplot. Plot along the aquifer the dissolution rate (on Y Axis pane, set “Variable type” to “Reactant properties”, then choose “Dissolution rate, Quartz”) in volume percent of the aquifer per year, again at t = 30 yr.
once again to open a second instance of Xtplot. Plot along the aquifer the dissolution rate (on Y Axis pane, set “Variable type” to “Reactant properties”, then choose “Dissolution rate, Quartz”) in volume percent of the aquifer per year, again at t = 30 yr.
How does quartz dissolution affect silica concentration in the flowing groundwater? How does silica accumulating in the groundwater affect the distribution of the quartz dissolution reaction?
Leaving the two instances of Xtplot alive, return to X1t and increase the time span
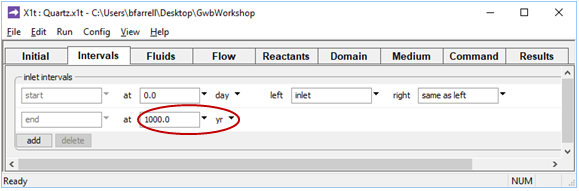
from 30 to 1000 years. This change has the effect of prescribing slower groundwater flow, since the pore fluid will still be displaced 100 times. Now, vx = (100 m)/(1000 yr/100) = 10 m yr−1.
Rerun the simulation. When the calculation finishes, the graphs you made in Xtplot will update themselves automatically. How has the distribution of the silica dissolution reaction changed in the aquifer?
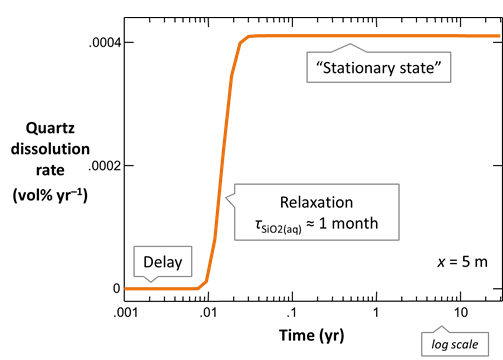
Finally, repeat the calculation assuming a time span of 1 year, which corresponds to vx = 10, 000 m yr−1. How have your plots changed?
The figure below shows results calculated for velocities spanning the range considered. The simulations correspond to Damköhler numbers Da much less than 1 for rapid flow, to much greater than 1 when flow is slow
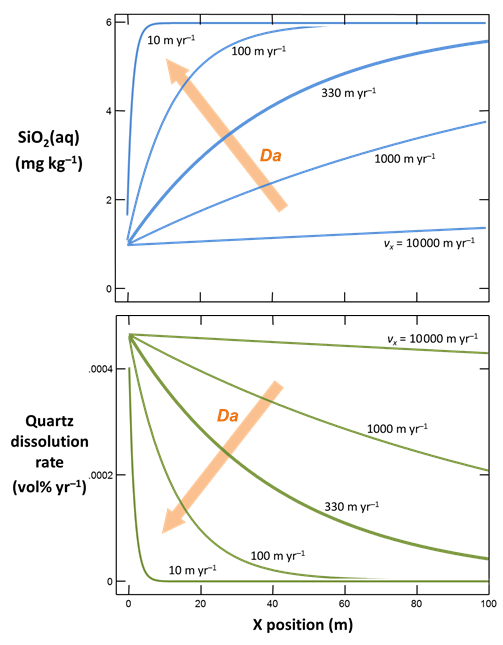
At low Da, transport overwhelms reaction and the fluid across the domain remains fully undersaturated with respect to quartz. Since quartz saturation changes little with position, the dissolution rate remains nearly constant. At high Da, in contrast, reaction controls transport and the infiltrating rainwater reacts toward equilibrium before migrating far from the inlet. In this case, the reaction rate is nearly 0 across most of the domain.
Only for the intermediate cases does silica concentration and reaction rate vary greatly across the main part of the domain. Significantly, only these cases benefit from the extra effort of calculating a reactive transport model.
For more rapid flows, the same result is given by a lumped parameter simulation, or box model, as we could construct in React. And for slower flow, a local equilibrium model suffices.
Animation of two-dimensional example
In an application of mineral dissolution and precipitation kinetics, hot water is injected into a petroleum reservoir in order to stimulate production. The steam flood reacts with kaolinite, calcite, and quartz in the formation to produce swelling clay (beidellite) and CO2.
The animations in the clip show variation over the course of the flood in:
- Temperature
- CO2 fugacity
- Percent swelling clay
- Formation permeability, accounting for the clay produced
Authors
Craig M. Bethke and Brian Farrell. © Copyright 2016–2026 Aqueous Solutions LLC. This lesson may be reproduced and modified freely to support any licensed use of The Geochemist's Workbench® software, provided that any derived materials acknowledge original authorship.
References
Bethke, C.M., 2022, Geochemical and Biogeochemical Reaction Modeling, 3rd ed. Cambridge University Press, New York, 520 pp.
Bethke, C.M., B. Farrell, and M. Sharifi, 2026, The Geochemist's Workbench®, Release 18: GWB Reactive Transport Modeling Guide. Aqueous Solutions LLC, Champaign, IL, 191 pp.
Knapp, R.B., 1989, Spatial and temporal scales of local equilibrium in dynamic fluid-rock systems. Geochimica et Cosmochimica Acta 53, 1955–1964.
Lasaga, A.C. and D.M. Rye, 1993, Fluid flow and chemical reaction kinetics in metamorphic systems. American Journal of Science 293, 361–404.
Leamnson, R.N., J. Thomas, Jr. and H.P. Ehrlinger, III, 1969, A study of the surface areas of particulate microcrystalline silica and silica sand. Illinois State Geological Survey Circular 444, 12.
Rimstidt, J.D. and H.L. Barnes, 1980, The kinetics of silica-water reactions. Geochimica et Cosmochimica Acta, 44 1683–1700.
Comfortable with mineral dissolution and precipitation?
Move on to the next topic, Microbial Populations, or return to the GWB Online Academy home.